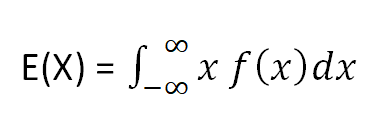Variance of a Continuous Random Variable
If X is a random variable having mean μ , then variance of random variable X is denoted as Var(X) and read as variance of X and defined as.
Var(X)=E[(X-μ)²]
Where
Variance of a random variable measures dispersion, that means how for values spread out from mean or expected value.
Var(X) can also be written as
Var(X)= E[X²] – [E[X]]²
See how it is derived
We have
Var(X)=E[(X-μ)²]
= E[X²+ μ²- 2 X μ]
= E[X²]+ E[μ²]- 2 E[ X ] E[μ]
=E[X²]+ E[μ²]- 2 E[ X ] E[μ]
= E[X²]+ μ²- 2 μ² Since μ=E[X]
= E[X²]+ – μ²
=Var(X)= E[X²] – [E[X]]²
Video: Variance of a Continuous Random Variable
Click to see pdf
Variance of continuous random variable
Properties of Variance of a Random Variable-
Find variance of a X + b i.e. Var(X)
We know that the variance of a random variable X is defined as
Var(X)= E[X²] – [E[X]]²
Then
Var ( a X + b) would be
Var(aX+b)= E[(aX+b)²] – [E[(aX+b)]]²
where E(X) can also be denoted by μ
The above expression can also be written as
Var(aX+b)= E[(a²X²+b²+2abX)]-[E(aX)+ E(b)]²
=E(a²X²)+E(b²)+E(2abX)-[aE(X)+ E(b)]²
=a²E(X²)+b²+2abE(X)-[aE(X)+ b]²
=a²E(X²)+b²+2abμ-[aμ+ b]²
=a²E(X²)+b²+2abμ-a²μ²-b²-2abμ
=a²E(X²)-a²μ²
=a²[E(X²)-μ²]
=a²[E[X²] – [E[X]]²]
=a²Var(X)
Case-1-
When a=5 and b=0
Var (5X+0)= 5²Var(X)
=25 Var(X)
This means that variance is sensitive to change of scale.
Case-2-
When a=0 and b=5
Var( 0 X+ 5)= Var(5)
Var(5)=0
This shows that variance of a constant is zero.
Case-3-
When a=1 b=5
Var(1. X+5)= 1² Var(X)= Var(X)
This implies that variance is independent of change of origin.
Video : Properties of Variance of a Random Variable-