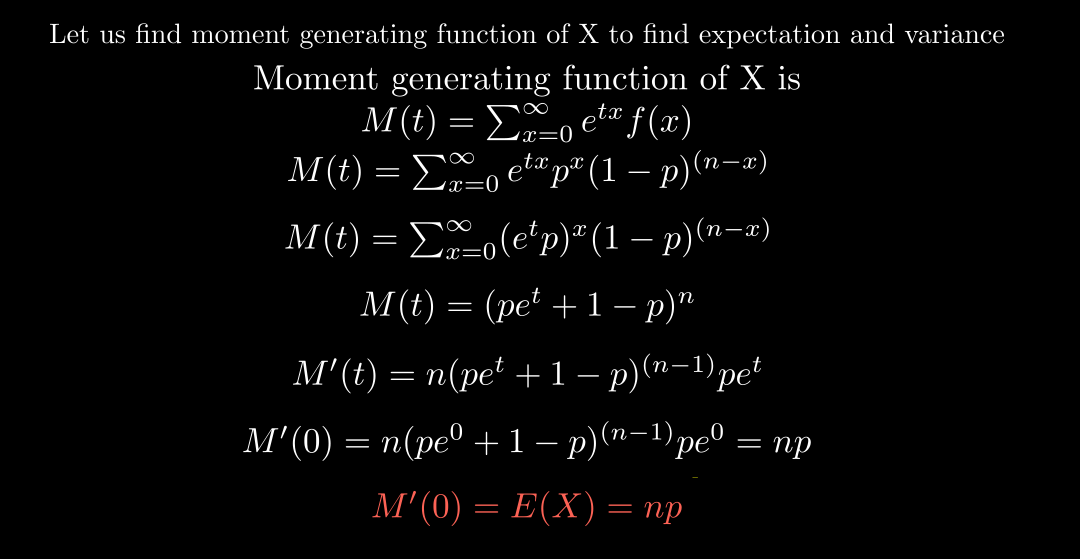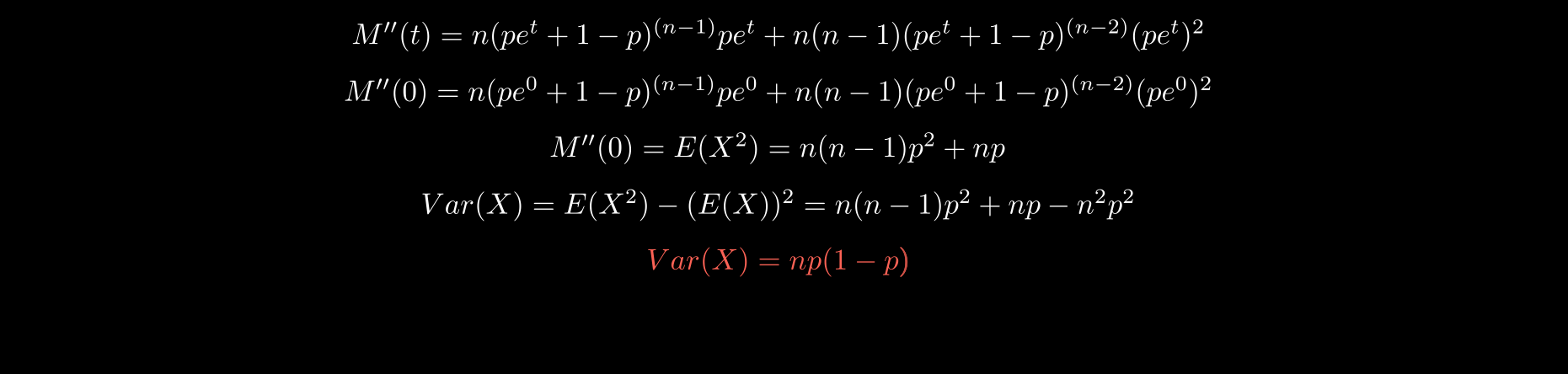Before understanding Binomial distribution you have to understand Bernoulli trial.
What is Bernoulli trial?
A Bernoulli trial is a random experiment in which there are two possible outcomes failure and success getting head when tossing a coin is success and getting tail is failure getting 4 is success when rolling a dice and failure when getting 1,2,3,5, and 6.
What is Binomial random variable?
A random variable X is called binomial random variable if it represents the total number of successes in n independent Bernoulli trials .
What is Binomial distribution?
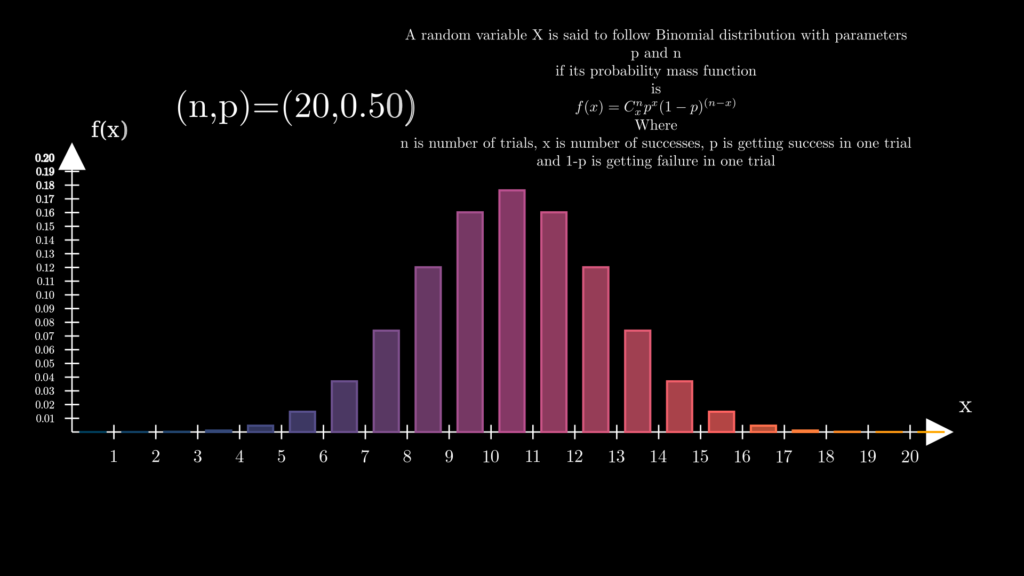
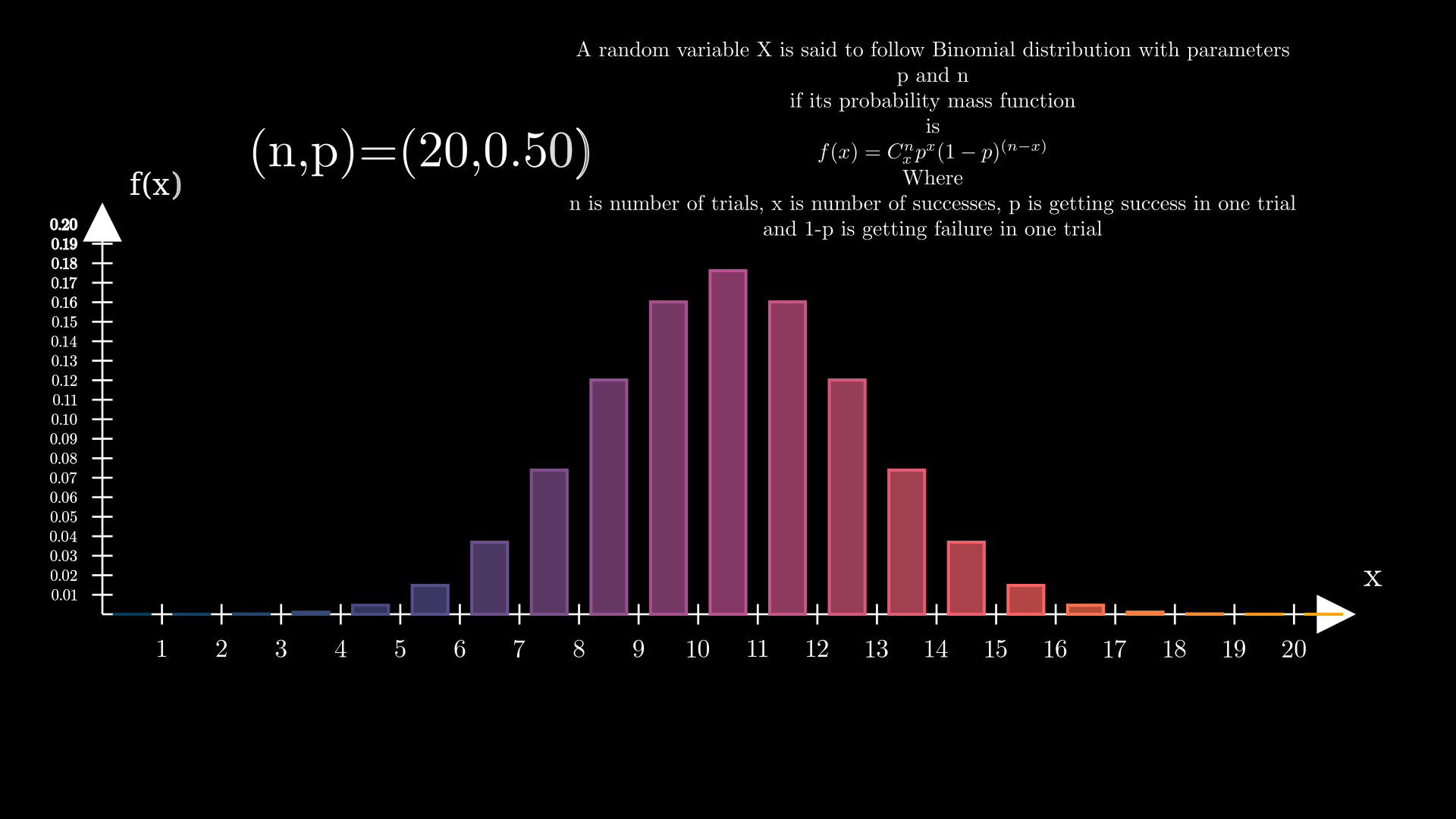
The binomial distribution is a probability distribution that describes the number of successes in a fixed number of independent Bernoulli trials, where each trial has only two possible outcomes: success or failure.
Expectation of a Random Variable-
The expectation (also known as the mean) of a binomial distribution is a measure of its central tendency. It represents the average or expected number of successes in a given number of independent trials.
See below, how Expectation of random variable X is calculated using Moment Generating Function.
Variance of a Random Variable-
The variance of a binomial distribution measures the dispersion (spread) of probabilities around the mean value. See below, how variance of random variable X is calculated using Moment Generating Function.
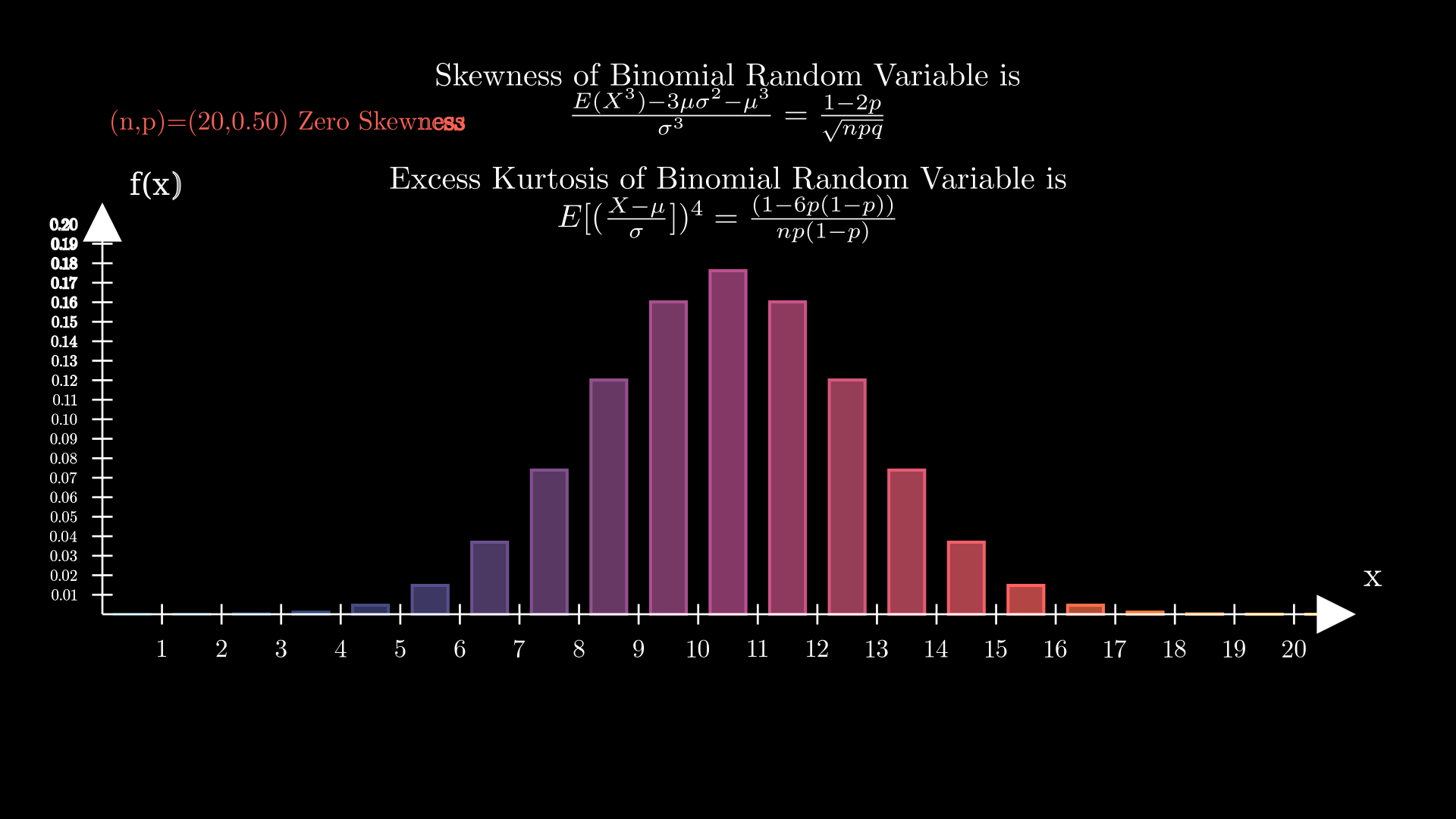
Skewness and Kurtosis-
Skewness:
Definition: Skewness refers to the degree of symmetry (or lack thereof) in a distribution.
Symmetry: A distribution is symmetric if it looks the same on both sides of its central point (mean or median).
Types of Skewness:
Positive Skewness: When the tail on the right side of the distribution is longer (extends farther) than the left tail. The distribution is skewed to the right.
Negative Skewness: When the left tail is longer than the right tail. The distribution is skewed to the left.
Zero Skewness: A perfectly symmetric distribution (rare in practice).
Kurtosis:
Definition: Kurtosis measures whether the data are heavy-tailed or light-tailed relative to a normal distribution.
Tails: It focuses on the tails of the distribution.
Types of Kurtosis:
Leptokurtic: A distribution with heavy tails (more data in the tails than a normal distribution). It has high kurtosis.
Platykurtic: A distribution with lighter tails (less data in the tails than a normal distribution). It has low kurtosis.
Mesokurtic: A normal distribution (standard kurtosis).
Interpretation:
If (n,p)=(20,0.70) then there is skewness present in the data distribution.
If (n,p)=(20,0.50) then there is no skewness present in the data distribution.
Watch the Video
References
https://en.wikipedia.org/wiki/Bernoulli_trial
https://www.cuemath.com/data/bernoulli-trials/