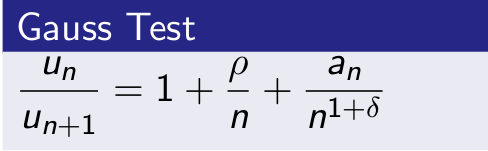Test for Convergence of Series

To understand test for  convergence of a series you have to understand sequence and series and related concepts.

Sequence

A sequence S is a function whose domain is natural numbers and range is real numbers.
i.e S: N->R. It is common practice to write a sequence S as S_n

Examples of Sequences-

S_n = <2n+1> = {3, 5, 7, 9, 11,……..}
S_n = <2n-1> = {1, 2, 5, 7, 9,……..}

Types of Sequence

Convergent Sequence-

Let S_n be a sequence, it is said to converge to a real number, if there exists a positive number \epsilon>0 and an integer m such that.
|S_n-l| < ε   n>=m  and n belongs to N.
Or it is written as Sn->l and read as S_n tends to l
where l is called limit of sequence Sn.

Example- S_n=<1/n> is converges to limit 0.

Divergent Sequence-

A sequence S_n is said to diverge if lim Sn-> ∞ or Sn-> -.
For example S_n= <2n + 1> diverges to +∞

Oscillatory Sequence-

A sequence S_n is said to an oscillatory sequence, if it neither converges nor diverges.
Sequence S_n= <(-1)ⁿ> neither converges nor diverges.
This sequence oscillates from -1 to +1.

Series-

A series is basically sum of elements of a sequence or more operations may involve with summation in series.

For example-
3+5+7+9+11+……………………… only summation is involved.
1+(1/2)+(1/3)+(1/4)+(1/5)+……………….. summation and division are involved.
1-(1/2)+(1/3)-(1/4)+(1/5)-(1/6)……………….. summation, subtraction and division are involved.

Test of convergence of a series.

To test weather a series converges to a limit or diverges is called test for convergence of series.
To test a series weather it converges or or diverges there or many methods are available.
If one test fails to recognize weather it converges or diverges another method you have to try.

D’ Alembert Ratio Test for Convergence –

Let ∑ u_n be the series of positive terms
Then

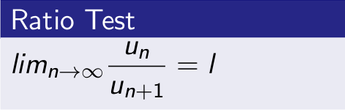
1- The series will be convergent, if l>1
2- The series will be divergent, if l<1
3- Test fails if l=1

Raabe’s   Test for Convergence –

Let ∑ u_n be the series of positive terms
Then

1- The series will be convergent, if l>1
2- The series will be divergent, if l<1
3- Test fails if l=1

Cauchy’s Root Test

Let ∑ u_n be the series of positive terms

Then

1- The series will be convergent, if l<1
2- The series will be divergent, if l>1
3- Test fails if l=1

Logarithmic Test for Convergence-

Let ∑ u_n be the series of positive terms
Then

1- The series will be convergent, if l>1
2- The series will be divergent, if l<1
3- Test fails if l=1

De Morgan’s and Bertrand’s Test for Convergence

Let \Sum u_n be the series of positive terms
Then

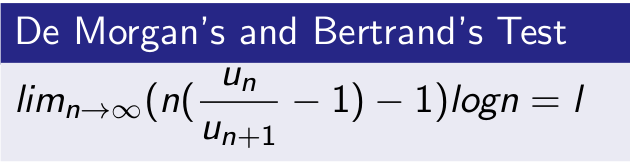
1- The series will be convergent, if l>1
2- The series will be divergent, if l<1
3- Test fails if l=1

Second Logarithmic Ratio Test for Convergence

Let ∑ u_n be the series of positive terms
Then

1- The series will be convergent, if l>1
2- The series will be divergent, if l<1
3- Test fails if l=1

Gauss’s Test for Convergence

Let ∑ u_n be the series of positive terms

Then

where ρ and δ are positive numbers and a_n is bounded sequence.
Series converges if ρ >1 and diverges if ρ <=1

---

 

Conclusion-

In this post, I have explained about  sequence, series and their test for  convergence  which is very important topic in mathematics.  Hope you will understand the concepts.