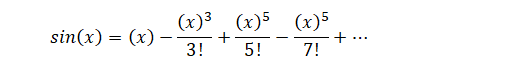Taylor’s theorem states that we can get expansion of a function f(x) at x=a
This can be written as
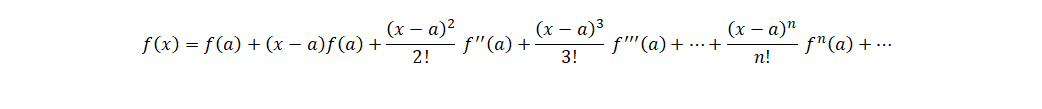
When we put a=0 it becomes Maclaurin’s series, and it has a lot of applications in mathematics and other areas.
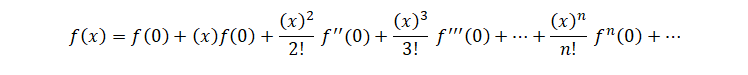
If you want expansion of ex you will require to find f(0), f’(0), f’’(0), f’’’(0), …………., fn (0)……..
And fortunately we will get
f(0)= f’(0)=f’’(0)=f’’’(0)=…….=f n (0)……=1
After putting these values in the above equation we will get
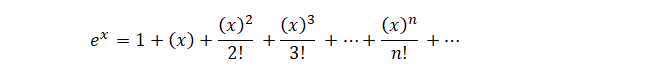
The same way we can find out the expansion of sin(x), after calculating
f(0), f’(0), f’’(0), f’’’(0), …………., n (0)……..
Here f(0)=sin(0)=0
f’(x)= cos(x) and f’(0)=cos(0)=1
f’’(x)=-sin(x) and f’’(0)=-sin(0)=0
f’’’(x)=-cos(x) and f’’’(0)=-cos(0)=-1
f’’’’(x)=sin(x) and f’’’’(0)=sin(x)=0
f’’’’’(x)=cos(x) and f’’’’’(0)=1
………………………………………………..
…………………………………………………
And if we put the above in Maclaurin’s series we will get the following series.