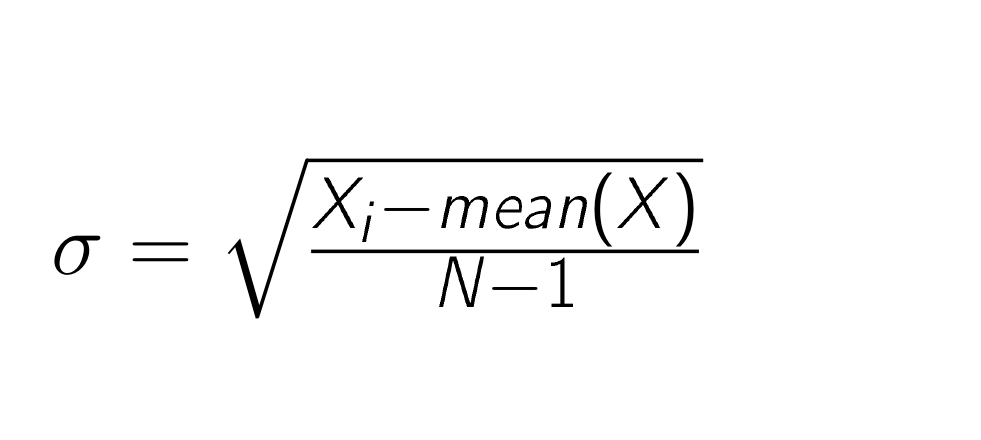Standard Deviation Variance and Covariance

Standard deviation, variance and covariance have very important applications in machine learning and data science. Further, they are closely related to each other. In feature reduction techniques, such as PCA ( Principle Component Analysis) features are selected based on  high variance.  In this post I will explain standard deviation, variance and covariance. I will also demonstrate how to compute standard deviation, variance and covariance in Python.

Standard Deviation

Standard deviation shows how data is spread about mean.  In other words, it measures the scantness  in a data set.

It is denoted by  σ and formula for standard deviation is

σ =  √|x_i-mean|/(n-1)

x_i is data series

n is the number of  data points

Python Code for  Standard Deviation

import statistics
data = [5,15,25,35,45]
sd=statistics.stdev(data)
m=statistics.mean(data)
print(“Mean”,m)
print(“Standard Deviation”,sd)

Output :

Mean 25
Standard Deviation 15.811388300841896

 

Variance

Variance is square of standard deviation which is

Variance=  σ²

Python Code for Variance

import statistics
data = [5,15,25,35,45]
sd=statistics.stdev(data)
m=statistics.mean(data)
v= statistics.variance(data)
print(“Mean”,m)
print(“Standard Deviation”,sd)
print(“Variance”,v)

Output:

Mean 25
Standard Deviation 15.811388300841896
Variance 250

Covariance

Covariance is  used to  measure variability between two variables. Suppose X and Y be two variables then covariance between X and Y is

Cov(X,Y) = (X-MeanX) (Y-MeanY)/ n-1

Let us calculate covariance matrix  in Python

Python Code for Covariance Matrix

import numpy as np
data = np.array([[5,15,25,35,45,65],[20, 35,40,50,60,70] ])
covmat=np.cov(data)
print(“Covarinace Matrix of X and Y”, covmat)

Output:

Covarinace Matrix of X and Y

[[466.66666667 383.33333333]
[383.33333333 324.16666667]]

Conclusion-

In this post, we have explained about standard deviation, variance, and covariance. These concepts are very useful applications in machine learning, data science and data analytics. Hope it is  useful for you and you will apply.

References-

• Detecting outliers: Do not use standard deviation around the mean, use absolute deviation around the median, Web Link, Retrieved on 09-10-2019, https://www.semanticscholar.org/paper/Detecting-outliers%3A-Do-not-use-standard-deviation-Leys-Ley/5935f52caf1df059ed9e301ad1fbfbd8d01bfa18.
• Dempster, A.P., 1972. Covariance selection. Biometrics, pp.157-175.
• Searle, S.R., Casella, G. and McCulloch, C.E., 2009. Variance components (Vol. 391). John Wiley & Sons.
• Kim, K., 1996. Face recognition using principle component analysis. In International Conference on Computer Vision and Pattern Recognition (Vol. 586, p. 591).