Random Variable and Probability Mass Function

Random variable  

is a very  important concept in probability, statistics, data science and machine learning, one must  learn concept of random variable and related concepts. In this post, I have explained random variable and probability mass function that will help you to have basic understanding of  random variable and probability mass function.
To understand random variable and probability mass function, first of all consider a random experiment in which three coins are tossed.
Then you will get the following outcomes
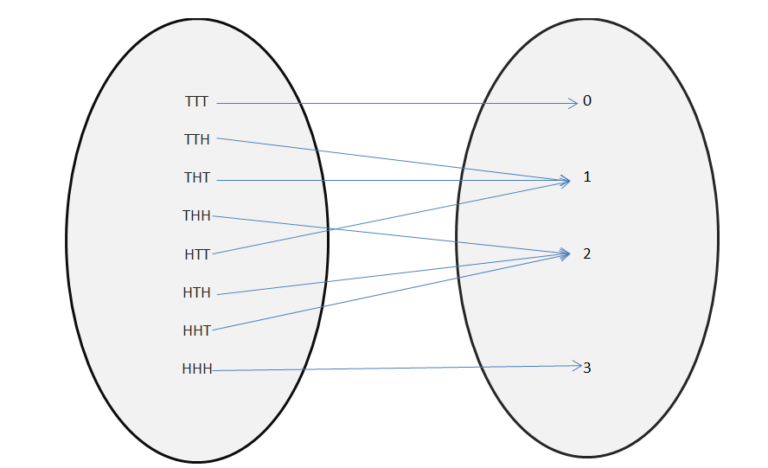
S={HHH, HHT,HTH,THH,TTH,THT,HTT,TTT}
Where
S–> Sample Space
H–> Occurence of head
T–> Occurence of tail

Let us define random variable
A random variable is a function from sample space pace S into the set of real numbers i.e. X: S->R_X, where R_X is the range of X.
Now define a random variable X(s)=Number of heads where s is an event in sample space S.
You will have X(HHH)=3, X(HHT)=2, X(HTH)=2, X(THH)=2, X(HTT)=1, X(THT)=1,(TTH)=1,X(TTT)=0
You can say a random variable is used to quantify sample space.

Probability mass function

f:R_x→R defined by  f(x)=P(X=x) is probability mass function of X.

Then

f(0)=P(X=0)= 1/8,  f(1)=P(X=1)= 3/8, f(2)=P(X=2)= 3/8,  f(3)=P(X=3)=1/8

Probability mass function f(x) has the following properties

1. f(x)≥0
2. Σ_xf(x)=1

Watch the the video