For large value of n binomial distribution asymptotically tends to Poisson distribution.
Probability distribution function of binomial random variable is

Probability distribution of Poisson random variable is
Poisson Distribution as a Limiting Case of Binomial Distribution
Python Code for Binomial Distribution
from scipy.stats import binom
import numpy as np
import matplotlib.pyplot as plt
# Let lambda=np=5
x = np.arange(0,10)
n=50
p=0.10
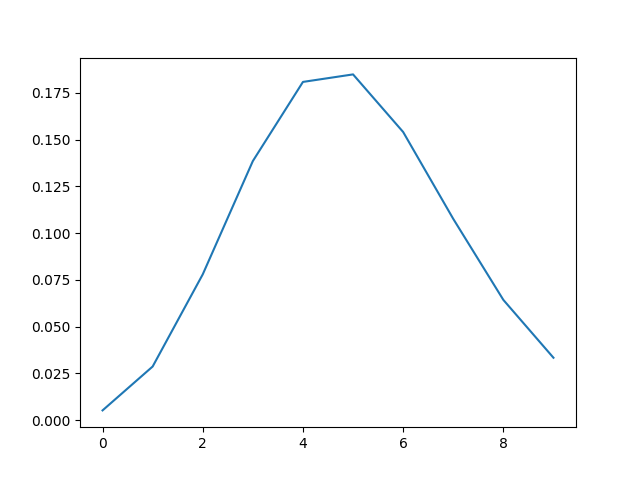
plt.plot(x, binom.pmf(x, n, p))
plt.savefig(“binom.png”)
For n=50 and p=0.10 and λ=5 x=0…..10
The plot is
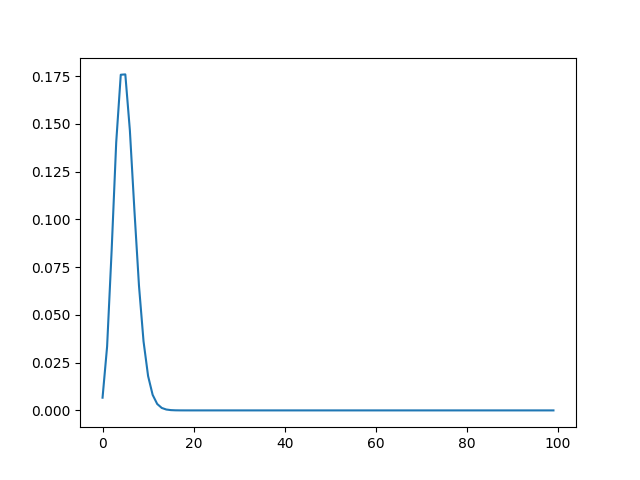
For n=1000 and p=0.005 where λ=5 and x=0…..100
from scipy.stats import binom
import numpy as np
import matplotlib.pyplot as plt
# Let lambda=np=5
x =np.arange(0,100)
n=1000
p=0.005
plt.plot(x, binom.pmf(x, n, p))
plt.savefig(“binom.png”)
Conclusion
In this post, I have derived probability distribution function of Poisson distribution using Stirling formula. Further, using Stirling formula many distributions can be derived in limiting case. Moreover, I hope you will also derive another distributions.