Linear Regression using Gradient Decent

Linear regression

Linear regression  is a supervised learning algorithm and tries to learn a  linear function from a given data set
D={(x_i, y_i)} where i=1, 2, 3, 4,———–N  where  x_i is feature vector and
y_i is target output. In other words, you will try to find out relationship between x_i and y_i.

Suppose you want to estimate a line  y=w x + b using a data set D, where w and b are linear regression model parameters. Basically, you want to find out the value of w and b such that the total error is minimum.

Furthermore, we will use a cost function or loss function which will measure how well a model performs.

We will use mean  squared   loss function which is

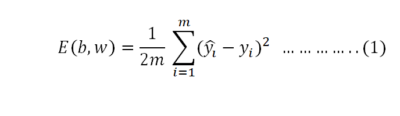
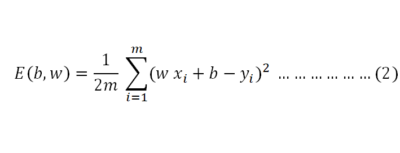
Where

The problem is to find   the     value of b and w such that   the   below   expression’s   value   is   minimum.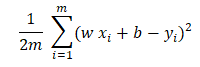

To find the minimum value of the above mean squared function we will use Gradient Decent algorithm.

What is Gradient Decent algorithm?

Gradient Decent algorithm is an optimization algorithm which finds minimum value of a differentiable function stepping gradient iteratively towards opposite direction.

It will find the value  using below equation

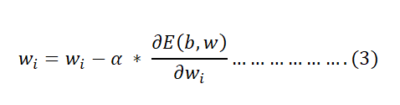
Where    $\alpha$  is learning rate and has range between 0 and 1.

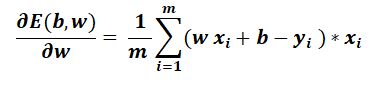
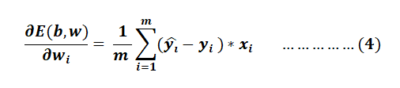
Then

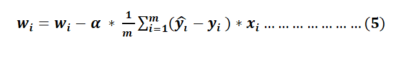
Similarly we can find

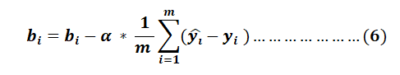
Values of b_i  and w_i  will get updated simultaneously.

 

References

1. Burkov, A. (2019). The hundred-page machine learning book (Vol. 1, p. 32). Quebec City, QC, Canada: Andriy Burkov.
2. Mitchell, T. M., & Mitchell, T. M. (1997). Machine learning (Vol. 1, No. 9). New York: McGraw-hill.
3. Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep learning. MIT press.
4. Hastie, T., Tibshirani, R., Friedman, J. H., & Friedman, J. H. (2009). The elements of statistical learning: data mining, inference, and prediction (Vol. 2, pp. 1-758). New York: springer.
5. Ruder, S. (2016). An overview of gradient descent optimization algorithms. arXiv preprint arXiv:1609.04747.
6. https://people.seas.harvard.edu/~yaron/AM221-S16/lecture_notes/AM221_lecture9.pdf