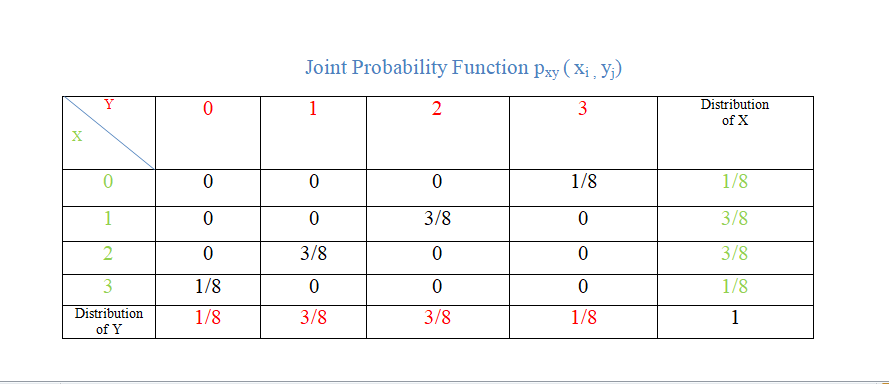
Joint and Marginal Probability Mass Function For UploadingIf (X,Y) is a two-dimensional discrete random variable, then joint probability mass function of  X and Y denoted by p_xy  and is defined as

p_xy(x_i,y_j)=P(X=x_i,Y=y_j)

If you toss three coins the following sample space you will get.

S={TTT, TTH, THT, THH, HTT, HTH, HHT,HHH}

X—- Occurrence of heads

Y—- Occurrence of tails

X={0, 1, 2, 3}

Y={0, 1, 2, 3}

Probabilities of events will be

P(X=0)=1/8,   P(X=1)=3/8,   P(X=2)=3/8,   P(X=3)=1/8

P(Y=0)=1/8,   P(Y=1)=3/8,   P(Y=2)=3/8,   P(Y=3)=1/8

And joint probabilities are

P(X=0,Y=0)=0

P(X=0,Y=1)=0

P(X=0,Y=2)=0

P(X=0,Y=3)= 1/8

P(X=1,Y=0)=0

P(X=1,Y=1)=0

P(X=1,Y=2)=3/8

P(X=1, Y=3)=0

P(X=2, Y=0)=0

P(X=2, Y=1)=3/8

P(X=2, Y=2)=0

P(X=2, Y=3)=0

P(X=3, Y=0)=1/8

P(X=3, Y=1)=0

P(X=3, Y=2)=0

P(X=3, Y=3)=0

Y X	0	1	2	3	Distribution of Y
0	0	0	0	1/8	1/8
1	0	0	3/8	0	3/8
2	0	3/8	0	0	3/8
3	1/8	0	0	0	1/8
Distribution of Y	1/8	3/8	3/8	1/8	1

Marginal Probability Mass Function of X

p_x(0) = p_xy(0,0) + p_xy(0,1) + p_xy(0,2) + p_xy(0,3) = 0+0+0+1/8= 1/8

p_x(1) = p_xy(1,0) + p_xy(1,1) + p_xy(1,2) + p_xy(1,3) = 0+0+3/8+0= 3/8

p_x(2) = p_xy(2,0) + p_xy(2,1) + p_xy(2,2) + p_xy(2,3) = 0+3/8+0+0= 3/8

p_x(3) = p_xy(3,0) + p_xy(3,1) + p_xy(3,2) + p_xy(3,3) = 1/8+0+0+0= 1/8

Marginal Probability Mass Function of Y

p_y(0) = p_xy(0,0) + p_xy(1,0) + p_xy(2,0) + p_xy(3,0) = 0+0+0+1/8= 1/8

p_y(1) = p_xy(0,1) + p_xy(1,1) + p_xy(2,1) + p_xy(3,1) = 0+0+3/8+0= 3/8

p_y(2) = p_xy(0,2) + p_xy(1,2) + p_xy(2,2) + p_xy(3,2) = 0+3/8+0+0= 3/8

p_y(3) = p_xy(0,3) + p_xy(1,3) + p_xy(2,3) + p_xy(3,3) = 1/8+0+0+0= 1/8

PDF File

Joint and Marginal Probability Mass Function