How to Compute Quartiles from Given Data
In this post, we will learn how to compute the quartiles \( Q_1 \), \( Q_2 \) (Median), and \( Q_3 \) using the provided data set. Quartiles help in dividing a data set into four equal parts, making it easier to understand the distribution of data. Let’s go step by step with the following data:
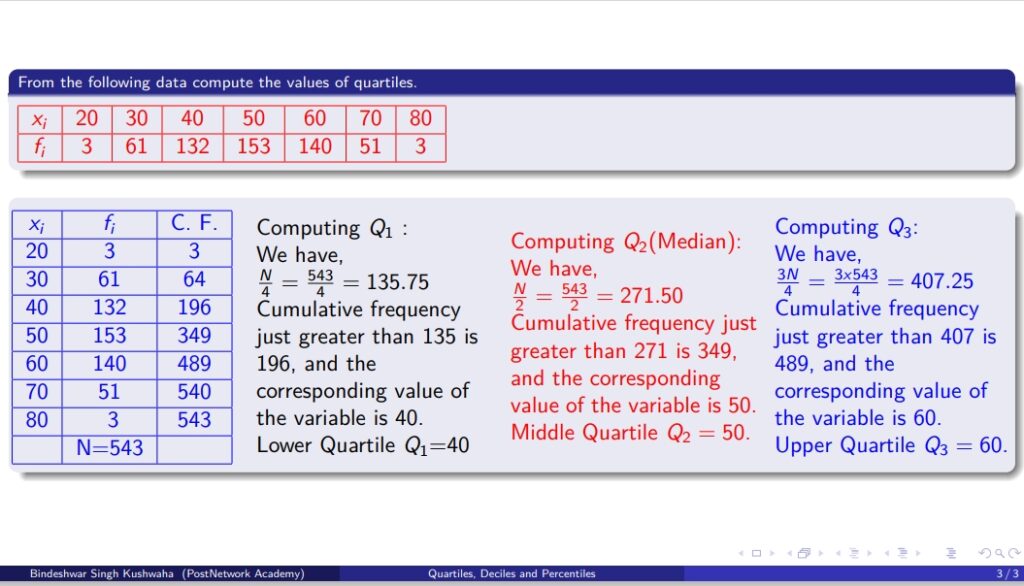
Data Set:
– \( x_i \): 20, 30, 40, 50, 60, 70, 80
– \( f_i \): 3, 61, 132, 153, 140, 51, 3
– \( N = 543 \) (Total frequency)
| \( x_i \) | \( f_i \) | Cumulative Frequency (C.F.) |
|---|---|---|
| 20 | 3 | 3 |
| 30 | 61 | 64 |
| 40 | 132 | 196 |
| 50 | 153 | 349 |
| 60 | 140 | 489 |
| 70 | 51 | 540 |
| 80 | 3 | 543 |
Step 1: Computing \( Q_1 \) (Lower Quartile)
To find the first quartile \( Q_1 \), we use the formula:
\[
Q_1 = \frac{N}{4} = \frac{543}{4} = 135.75
\]
The cumulative frequency just greater than 135 is 196, and the corresponding value of the variable is \( 40 \).
Thus, Lower Quartile \( Q_1 = 40 \)
Step 2: Computing \( Q_2 \) (Median)
The second quartile or median is computed using:
\[
Q_2 = \frac{N}{2} = \frac{543}{2} = 271.50
\]
The cumulative frequency just greater than 271 is 349, and the corresponding value of the variable is \( 50 \).
Thus, Median \( Q_2 = 50 \)
Step 3: Computing \( Q_3 \) (Upper Quartile)
For the upper quartile, we compute:
\[
Q_3 = \frac{3N}{4} = \frac{3 \times 543}{4} = 407.25
\]
The cumulative frequency just greater than 407 is 489, and the corresponding value of the variable is \( 60 \).
Thus, \Upper Quartile \( Q_3 = 60 \).
PDF Presentation
quartilefreqdis
Video
Quiz