Exponential Distribution Formula
A random variable X is said to follow Exponential distribution if it has the following probability density function
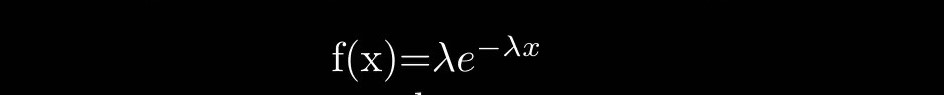
the value f(x) is zero when x < 0 otherwise it is equal to f(x).
Moment Generating Function
The moment generating function (MGF) is a powerful tool in probability theory and statistics used to derive moments of a probability distribution.
The moment generating function is particularly useful because of the following properties:
- Uniqueness: If two random variables have the same moment generating function, then they have the same probability distribution.
- Derivatives: Moments can be easily derived by taking derivatives of the moment generating function.
- Convolution: For independent random variables, the moment generating function of their sum is the product of their individual moment generating functions.
- Relation to Cumulant Generating Function: The logarithm of the moment generating function is called the cumulant generating function, and it provides information about cumulants, which are related to moments.
In summary, the moment generating function is a mathematical tool used to study the moments of a probability distribution, providing a convenient way to derive and analyze statistical properties of random variables.
Expectation and Variance of Exponential Random Variable
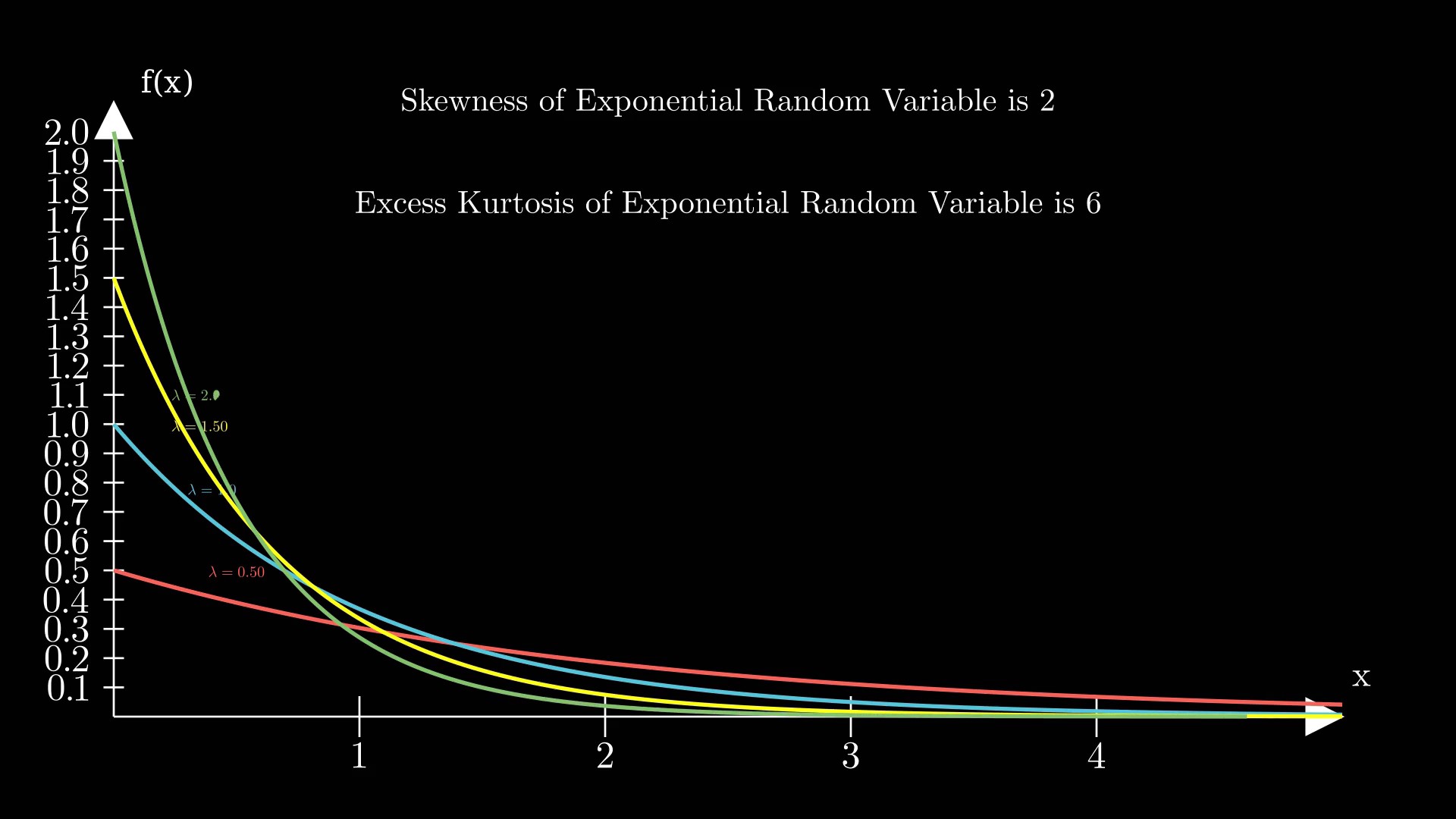
The exponential distribution is often used to model the time until an event occurs in a wide range of real-world scenarios. It is characterized by a single parameter, typically denoted as λ (lambda), which represents the rate at which events occur.
- Skewness: The skewness of a distribution measures its asymmetry. For the exponential distribution, the skewness is: Skewness=2 Skewness = 2 The exponential distribution is positively skewed, meaning it has a tail that extends further to the right.
- Kurtosis: Kurtosis measures the “tailedness” of a distribution. For the exponential distribution, the kurtosis is: Kurtosis=6 Kurtosis = 6 This indicates that the exponential distribution has heavier tails compared to the normal distribution, which has a kurtosis of 3 (the kurtosis of a normal distribution is often defined as 0, but when calculated conventionally using the formula involving the fourth central moment, it’s 3).
These values are derived from the theoretical formulas for skewness and kurtosis for the exponential distribution. They are helpful in understanding the shape and characteristics of the distribution, particularly in comparison to other distributions.
The exponential distribution finds applications in various fields due to its ability to model the time between events in processes characterized by a constant rate of occurrence. Here are some common applications:
- Reliability Engineering: In reliability engineering, the exponential distribution is often used to model the time until failure of a system or component. It helps in understanding the reliability and lifetime of products and systems, aiding in maintenance scheduling and decision-making.
- Queuing Theory: Queuing theory deals with the study of waiting lines or queues. The exponential distribution is used to model the inter-arrival times or service times in queuing systems such as customer arrivals at a service point, traffic flow at intersections, or packet arrivals in computer networks.
- Telecommunications: In telecommunications, the exponential distribution is employed to model the duration between successive phone calls, data packet arrivals in networks, or the time until the next failure in a communication system. It helps in analyzing network performance and resource allocation.
- Inventory Management: Inventory management involves optimizing inventory levels to meet customer demand while minimizing costs. The exponential distribution can be utilized to model the time between orders or deliveries in inventory systems. It aids in determining reorder points and inventory replenishment strategies.
- Medical Sciences: In medical sciences, the exponential distribution is applied to model the survival times of patients, the time between occurrences of medical events (e.g., seizures), or the decay of radioactive substances in biological systems. It assists in clinical trial design, epidemiological studies, and understanding disease progression.
- Environmental Sciences: In environmental studies, the exponential distribution is used to model the time between occurrences of environmental events such as earthquakes, floods, or pollutant emissions. It helps in assessing risks, planning emergency responses, and studying natural phenomena.
- Financial Modeling: In finance, the exponential distribution can be employed to model the time until default of financial instruments, the duration between stock price movements, or the waiting times between trades. It facilitates risk management, option pricing, and portfolio analysis.
These are just a few examples of the diverse applications of the exponential distribution across different disciplines. Its simplicity and versatility make it a valuable tool for analyzing various processes involving the timing of events.
Watch the video
References
https://brilliant.org/wiki/exponential-distribution/