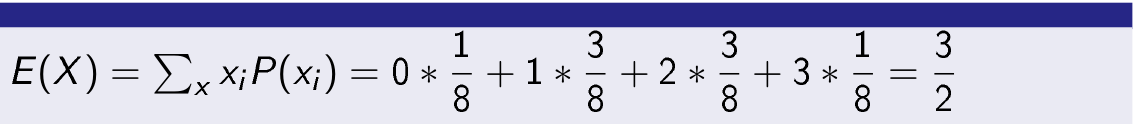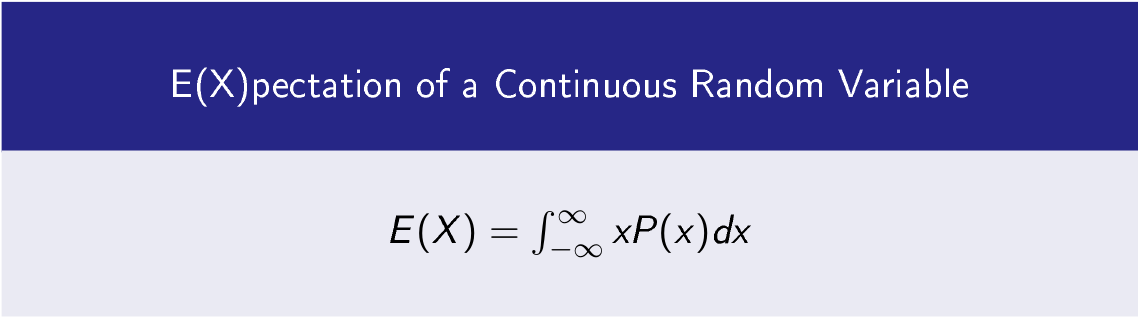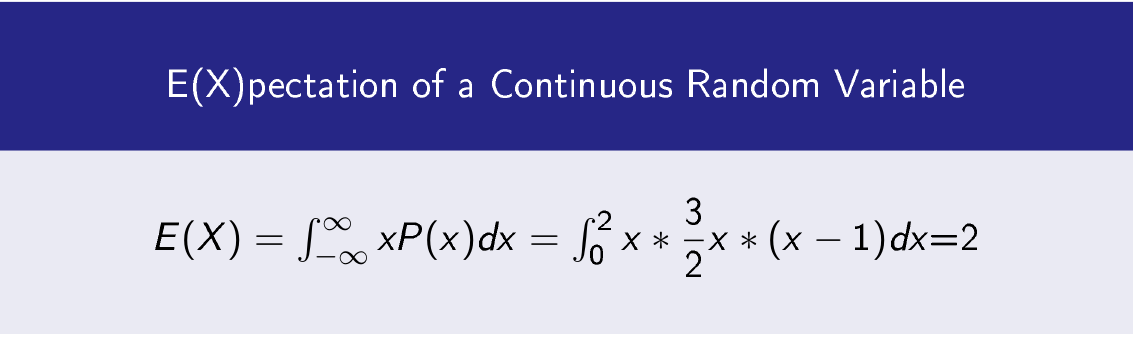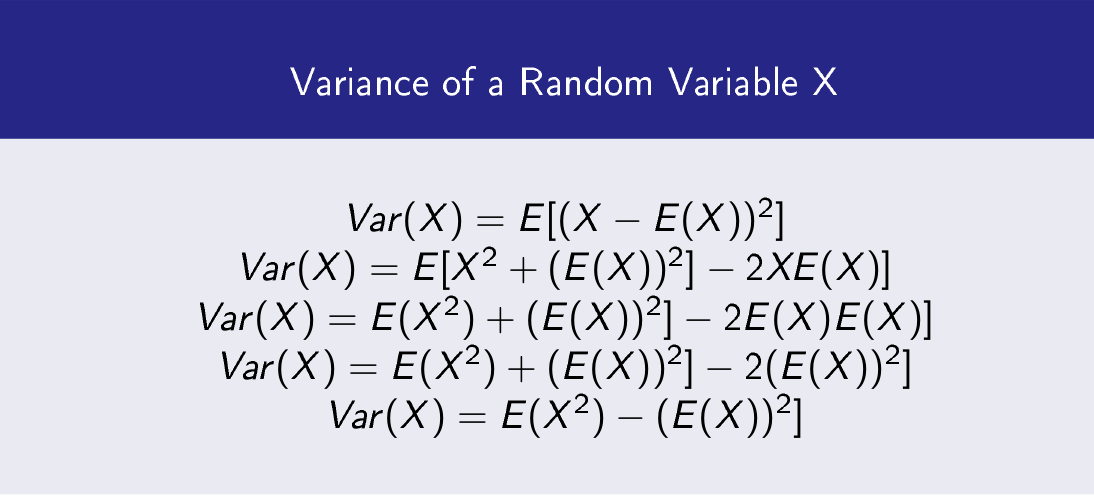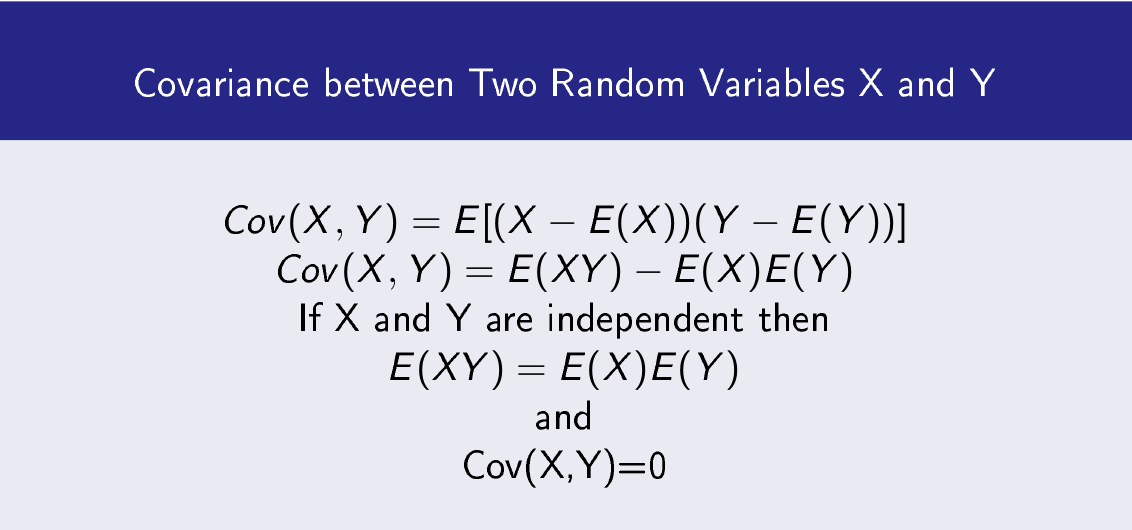Expectation in Statistics

Contents hide

Expectation in statistics is the weighted average of a random variable with its probability.

Suppose you toss three coins, then think of event to turn heads up.

Random variable associates number of occurrence of event to its probability.
i.e.
Expectation of random variable X is denoted by E(X).

1- Expectation of a Discrete Random Variable X

To understand expectation of a discrete random variable. Take an example of tossing of three coins.

The possible values when you toss three coins.
TTT
TTH
THT
THH
HTT
HTH
HHT
HHH

X(TTT)=0
X(TTH)=1
X(THT)=1
X(THH)=2
X(HTT)=1
X(HTH)=2
X(HHT)=2
X(HHH)=3

Then
P(X=0)=1/8
P(X=1)=3/8
P(X=2)=3/8
P(X=3)=1/8
Here, P(X) is probability distribution function of random variable X.

Then expression for expectation of a discrete random variable is.

Then expected value of random variable X is.

If X is a continuous random variable and p(x) is a continuous probability distribution function.

Then expectation of continuous random variable X is.

Let p(x) be defined as

p(x)=3/2 x(x-1) 0<=x<=2
for a random variable X.

Then expectation of continuous random variable X is

If X and Y are independent random variables
1- E(X+Y)= E(X) + E(Y)
2- E(X.Y)= E(X) E(Y)
3- Is a is a and b are constants then
1- E(aX+b)= a E(X) + b

Variance of a random variable is X

Covariance between Two Random Variables X and Y is