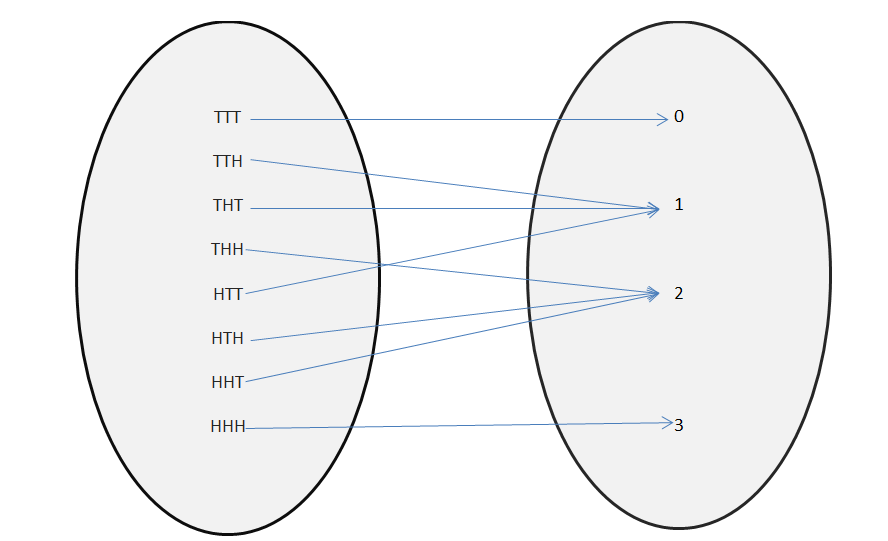
A random variable X is a function from a sample S to real numbers R, i.e X: S——>R. Suppose you are tossing three coins then the sample space would be.
S={HHH,TTH, THT, THH, HTT, HTH, HHT, HHH}
Then X maps sample space to real numbers.
Where you can see that R={0,1,2, 3}
You can also write probability distributions
f(0)= P(X=0)= 1/8
f(1)= P(X=1)= 3/8
f(2) = P(X=2)=3/8
f(3)= P(X=3)=1/8
P(X=0) denotes probability of 0 HEAD
P(X=1) denotes probability of one HEAD
P(X=2) denotes probability of two HEADs
P(X=3) denotes probability of three HEADs
And function f is probability density function, a probability density function has two properties.
(1)- f(x)≥0
(2) Σx f(x)=1 = 1/8+3/8+3/8+1/8
Expectation of a discrete random variable is defined as composition of random variable values weighted by the corresponding probabilities.
i.e.
E(X)= 0. (1/8 )+ 1. (3/8)+ 2. (3/8) + 3.(1/8)
E(X)=12/8=3/2=1.5
See video to understand above video
