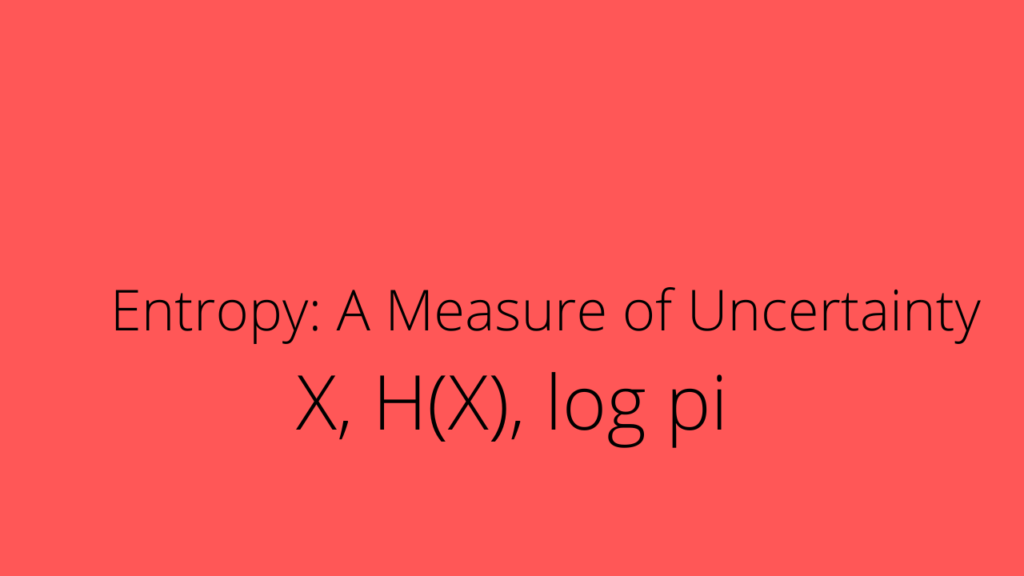Entropy: A Measure of Uncertainty

Entropy of a random  variable measures uncertainty  inherent to possible outcomes of the variable.

H(X)= -Σ_iⁿ    p_ilog₂p_i , where i=1, 2, 3 , 4, …..,n

Where p_i  are probabilities of associated events.

Take an example of tossing two coins, then you will have sample space .

S={T,H}

And X is defined as number of heads.

Then

P(X=0)=1/2 ———->Probability  of getting 0 head.

P(X=0)=1/2 ———->Probability  of getting 1 head.

Then

H(X)= -[1/2 log₂1/2+1/2 log₂1/2]= 1 bit

Now increase the probability of getting head from 1/2 to 2/3.

Then probability of getting tail will decrease  from 1/2 to 1/3.

and

H(X)= -[2/3 log₂2/3+1/3 log₂1/3]

H(X)= -[2/3* (-0.585)+1/3 * (-1.585)]=0.91 bit(s)

You can observe that  uncertainty is decreased from 1.0 bit(s) to 0.91 bits.

Again

Increase the probability of getting head from  2/3 to 3/4.

Then probability of getting tail will decrease  from 1/3 to 1/4.

and

H(X)= -[3/4 log₂3/4+1/4 log₂1/4]

H(X)= -[3/4* (-0.415)+1/4 * (-2)]=0.81 bit(s)

You can observe that  uncertainty is decreased from 0.91 bit(s) to 0.81 bits.

Finally, take the extreme case

Increase the probability of getting head from  3/4 to 1.

Then probability of getting tail will decrease  from 1/4 to 0.

and

H(X)= -[1 log₂ 1+0 log₂0]=0

It means that there is no uncertainty, because you have you increased the probability of getting head as 1. So, always head will come i.e. 0 uncertainty.

See the video tutorial