Hello everyone! Welcome back to Postnetwork Academy. I’m Bindeshwar Singh, and today we’re going to uncover a key concept in statistics that helps you understand data more deeply—deciles!
Have you ever wondered how to break down a data set into smaller, meaningful parts? Deciles allow us to split data into 10 equal sections, giving us a clearer view of its distribution. In this post, we’ll dive into a practical example, learning how to find the 3rd and 7th deciles in an easy, step-by-step way.
Deciles Calculation and Visualization
Author: Bindeshwar
Date:
1. Given Data Set and Decile Calculation
Given data set: 3, 6, 9, ... , 60
To find the 3rd and 7th deciles, we use the position formula:
\[
\text{Position of } D_k = \frac{k \cdot (n + 1)}{10}
\]
where n = 20.
2. 3rd Decile Calculation
The position of \( D_3 \):
\[
\text{Position of } D_3 = \frac{3 \cdot (20 + 1)}{10} = 6.3
\]
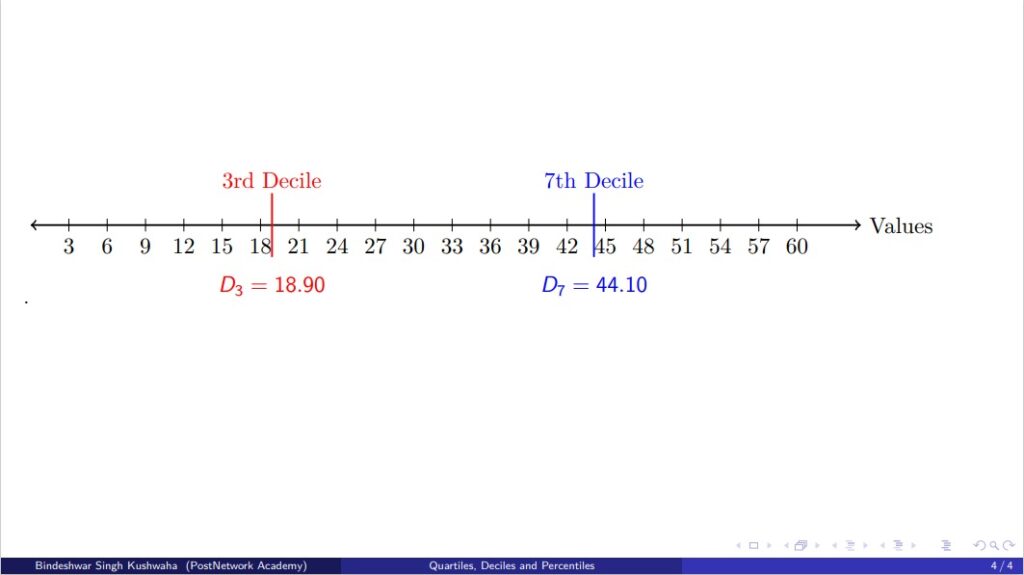
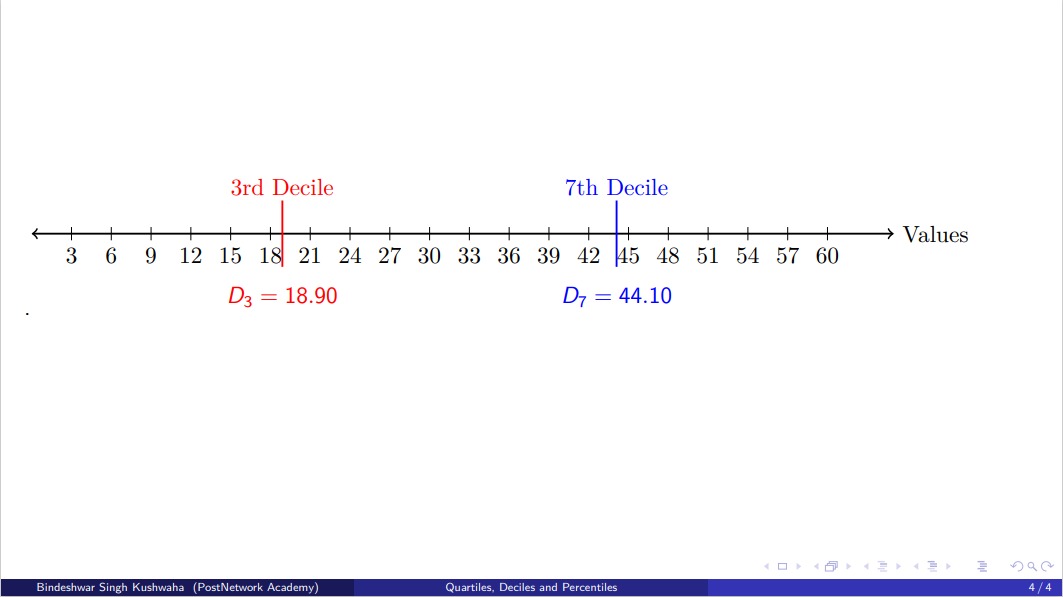
The 3rd decile, \( D_3 \), is located between the 6th and 7th values (18 and 21):
\[
D_3 = 18 + (0.3 \times (21 – 18)) = 18.9
\]
3. 7th Decile Calculation
The position of \( D_7 \):
\[
\text{Position of } D_7 = \frac{7 \cdot (20 + 1)}{10} = 14.7
\]
The 7th decile, \( D_7 \), is located between the 14th and 15th values (42 and 45):
\[
D_7 = 42 + (0.7 \times (45 – 42)) = 44.1
\]
4. Results
We conclude that:
- 3rd Decile (\( D_3 \)) = 18.9
- 7th Decile (\( D_7 \)) = 44.1
5. Visualization of Data Set with Deciles
Below is a representation of the number line with the positions of \( D_3 \) and \( D_7 \) marked: