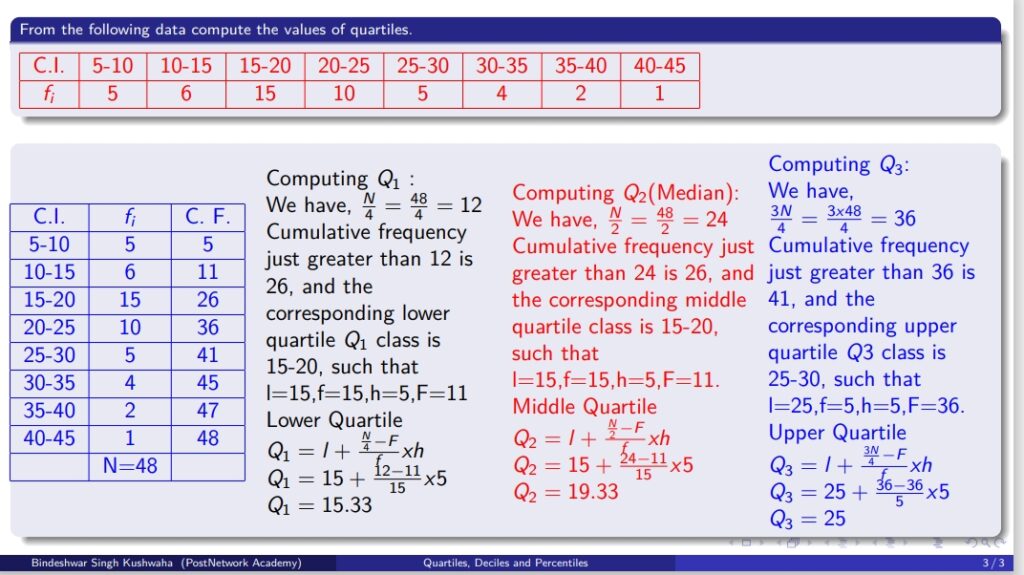
Quartiles help to divide a dataset into four equal parts. In this post, we will compute the values of the lower quartile (Q₁), median (Q₂), and upper quartile (Q₃) from a given set of grouped data.
Data:
| C.I. | fᵢ |
|——-|—–|
| 5-10 | 5 |
| 10-15 | 6 |
| 15-20 | 15 |
| 20-25 | 10 |
| 25-30 | 5 |
| 30-35 | 4 |
| 35-40 | 2 |
| 40-45 | 1 |
The cumulative frequency (C.F.) for this dataset is as follows:
| C.I. | fᵢ | C.F. |
|——-|—–|——|
| 5-10 | 5 | 5 |
| 10-15 | 6 | 11 |
| 15-20 | 15 | 26 |
| 20-25 | 10 | 36 |
| 25-30 | 5 | 41 |
| 30-35 | 4 | 45 |
| 35-40 | 2 | 47 |
| 40-45 | 1 | 48 |
Total N = 48.
Step-by-Step Quartile Calculation:
1. Lower Quartile (Q₁):
We calculate Q₁ using the formula:
\[
Q₁ = L + \left(\frac{\frac{N}{4} – F}{f}\right) \times h
\]
Where:
– L is the lower boundary of the Q₁ class
– N/4 = 48/4 = 12
– Cumulative frequency (F) just greater than 12 is 26, corresponding to the class 15-20.
– L = 15, f = 15, F = 11, h = 5.
Substituting the values:
\[
Q₁ = 15 + \left(\frac{12 – 11}{15}\right) \times 5 = 15 + \frac{5}{15} = 15.33
\]
2. Median (Q₂):
The median is calculated using:
\[
Q₂ = L + \left(\frac{\frac{N}{2} – F}{f}\right) \times h
\]
Where:
– N/2 = 48/2 = 24
– Cumulative frequency (F) just greater than 24 is 26, corresponding to the class 15-20.
– L = 15, f = 15, F = 11, h = 5.
Substituting the values:
\[
Q₂ = 15 + \left(\frac{24 – 11}{15}\right) \times 5 = 15 + 4.33 = 19.33
\]
3. Upper Quartile (Q₃):
We calculate Q₃ using:
\[
Q₃ = L + \left(\frac{\frac{3N}{4} – F}{f}\right) \times h
\]
Where:
– 3N/4 = 3 × 48/4 = 36
– Cumulative frequency (F) just greater than 36 is 41, corresponding to the class 25-30.
– L = 25, f = 5, F = 36, h = 5.
Substituting the values:
\[
Q₃ = 25 + \left(\frac{36 – 36}{5}\right) \times 5 = 25
\]
PDF Presentation
quartilescontinuousVideo
Conclusion:
The computed quartiles for the given data are:
– Lower Quartile (Q₁): 15.33
– Median (Q₂): 19.33
– Upper Quartile (Q₃):25