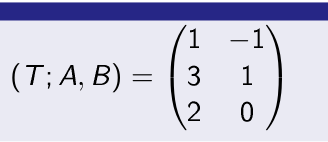Matrix Representation of a Linear Transformation

Matrix Representation of a Linear Transformation

Suppose U and V are two vector spaces over the same field F of dimensions m and n. Let A = {α₁, α₂, α ₃,……,α₃} and B={β₁, β₂, β₃,…….,β_n} be ordered bases of U and V.
If T is a linear transformation such that T:U->V and it is defined as

Example-

If a linear transformation which is defined as T(a,b)=(a-b, 3a+b, 2a) from T:V₂->V₃. Find out the matrix representation linear  of  a transformation T under the ordered bases
A={(1,0),(0,1)}
B={(1,0,0), (0,1,0), (0,0,1)}.

Solution-

T(1,0) = (1,3,2) = 1 (1,0,0) + 3 (0,1,0) + 2 (0,0,1)
T(0,1) = (-1,1,0)= -1 (1,0,0) + 1 (0,1,0) + 0 (0,0,1)

Then the matrix  of linear transformation T:V₂->V₃ related to ordered bases A and B is

Conclusion-

In this post, I have explained that how to find out matrix under a liner transformation related to ordered bases. Hope you will understand it.